Software

Variable-Density Sampling and Radial View-Ordering (VDRad)

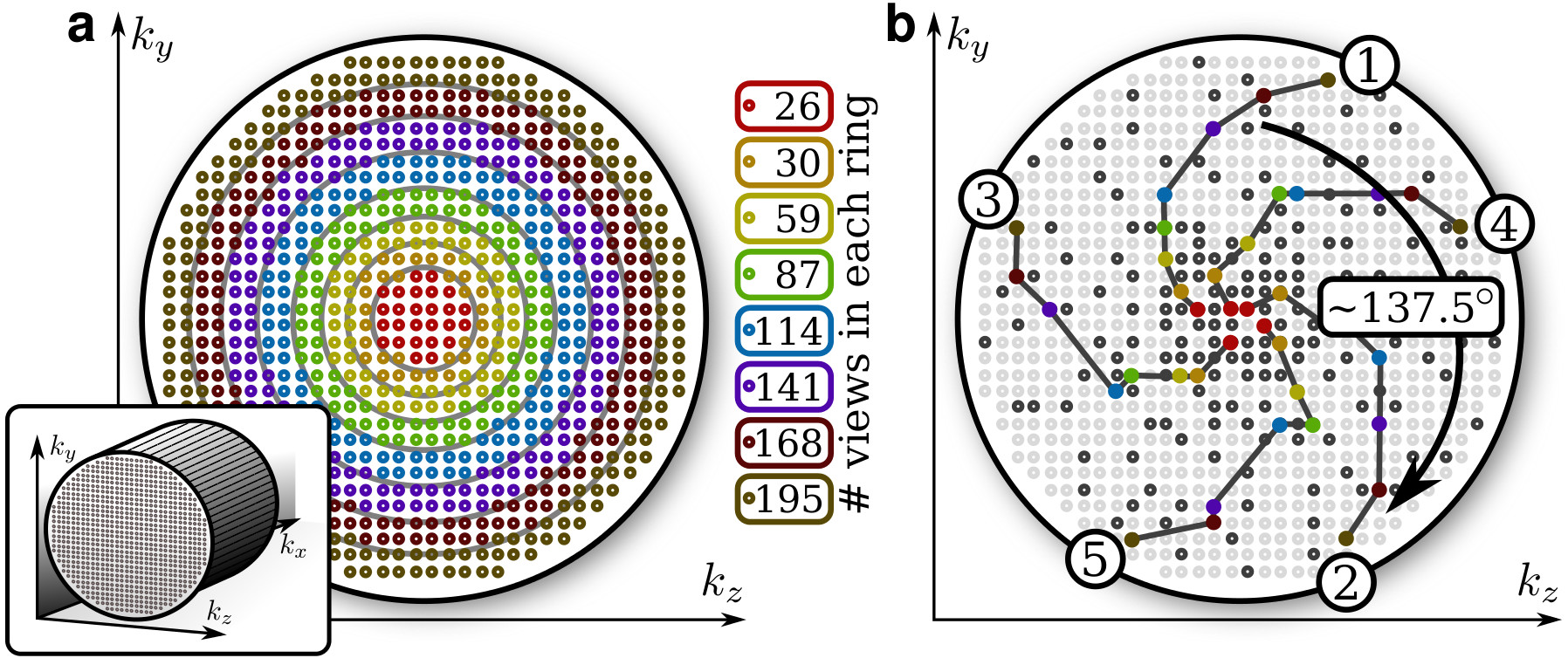For 3D Cartesian imaging, we focus the design of the data acquisition scheme on achieving motion-robustness and ideal undersampling patterns for accelerated imaging techniques. The technique that we have developed is the Variable Density sampling and Radial view-ordering, VDRad for short.

Because of the advantageous motion properties of radial imaging, we mimic the effects for 3D Cartesian imaging by grouping (ky,kz)-views into radial spokes. These spokes are ordered according to the Golden Ratio [4]. Lastly, we incorporate variable-density sampling for an ideal undersampling pattern for accelerated imaging. An important feature in our method is that we provide flexibility to support arbitrary (both isotropic and anisotropic) sampling patterns to cater to different hardware configurations.

The generated view-ordering/sampling pattern is also ideal for time-resolved acquisition techniques where it is important to have unique sampling patterns at each time point.

MATLAB Example

The MATLAB scripts/functions are included here to provide a way to illustrate the VDRad algorithm. Different sampling patterns and (both isotropic and anisotropic) accelerations can be prescribed to cater to arbitrary coil array configurations.

Downloads – MATLAB scripts/functions demonstrating VDRad

• VDRad_MATLAB_v0.2.zip (SHA-1) | DEMO

• VDRad_MATLAB_v0.1.zip (SHA-1) | DEMO

References

1. Cheng JY, Zhang T, Ruangwattanapaisarn N, Alley MT, Uecker M, Pauly JM, Lustig M, Vasanawala SS. “Free-breathing pediatric MRI with nonrigid motion correction and acceleration,” Journal of Magnetic Resonance Imaging 2014. doi: 10.1002/jmri.24785

2. Cheng JY, Uecker M, Alley MT, Vasanawala SS, Pauly JM, Lustig M. “Free-breathing pediatric imaging with nonrigid motion correction and parallel imaging.” In Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City, Utah, USA, 2013. p. 312.

3. Cheng JY, Zhang T, Alley MT, Lustig M, Vasanawala SS, Pauly JM. “Variable-density radial view-ordering and sampling for time-optimized 3D Cartesian imaging.” In Proceedings of the ISMRM Workshop on Data Sampling and Image Reconstruction, Salt Lake City, Utah, USA, 2013.

4. Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging 2007; 26:68–76.

(Updated 16 October 2014)

Nonrigid Motion Correction in 3D: Autofocusing

Because of the lengthy duration of typical MR scans, data acquired are sensitive to motion effects. There has been a lot of research on methods to minimize these motion artifacts – from prospective to retrospective methods. We wanted to focus on a method that can be generalized to any sequence. Thus, we worked on correcting for these artifacts retrospectively during the reconstruction process.

In order to do so, we looked into autofocusing (autocorrection). Some work has been published on this idea for the application of motion correction. By localizing the autofocusing process, we extend the concept to nonrigid motion artifacts. In order to make the algorithm computationally feasible, we limit the search space to motion paths to be linear paths collected with multi-channel receivers. The motion paths were estimated from navigator data collected using the Butterfly modification.

More details of the pulse sequence design and algorithm can be found in the references.

MATLAB Example

A complete MATLAB-based implementation can be downloaded. It is much slower than the OMP,CUDA,C++ version, but it demonstrates the key concepts of the algorithm. For more information, see the informative README file.

You can also download each file separately:

• MATLAB tools:

  • jycMatlabBfly_v0.2.zip – MATLAB functions that perform the motion estimation and the autofocusing correction.

  • jycMatlabUtil_v0.2.zip – extraneous MATLAB functions used by the other motion correction package.

• Example data:

  • example1.mat – anonymized in vivo dataset.

• MATLAB scripts:

  • demo.m – executes all other scripts

  • setupPath.m – setups the MATLAB paths.

  • runBflyMotionEstimate.m – performs the motion estimation from the Butterfly navigator data.

  • runMotionAutofocus.m – performs the motion correction using autofocusing.

Alternatively, the entire package can be downloaded in one ZIP file. The additional MATLAB tools needed are also included.

• jycMatlabBflyAll_v0.2.zip

(Added 24 Sept 2014 with old version)

References

1. Lustig M, Daniyaldaze E, Cunningham CH, Pauly JM. “Butterfly MRI: A Self Navigating Cartesian Trajectory,” ISMRM 2007.

2. Cunningham CH, Lustig M, Pauly JM. Self Navigating Cartesian Trajectory. US Patent 7,692,423. 2010 April 6.

3. Cheng JY, Alley MT, Cunningham CH, Vasanawala SS, Pauly JM, Lustig M. “Nonrigid Motion Correction in 3D Using Autofocusing with Localized Linear Translations,” Magnetic Resonance in Medicine 2012; 68: 1785-1797.

MATLAB Tools

In order to run some of the example code, you will need some additional MATLAB functions. You can download the additional tools here:

• jycMatlabUtil_v0.2.zip

In the archived file, you will find some debugging tools and common functions needed for typical MR reconstructions